Mixed Strategy Constraints in Continuous Games

Following past research regarding mixed-strategy robot interactions in continuous space, we investigated different ways of setting constraints in these settings without losing the strategic richness given by mixing.

Abstract

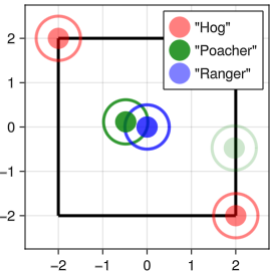
When modeling robot interactions as Nash equilibrium problems, it is desirable to place coupled constraints which restrict these inter- actions to be safe and acceptable (for instance, to avoid collisions). Such games are continuous with potential mixed strategy equilibria, and this combination of characteristics means special care must be given to setting coupled constraints in a way that respects mixed strategies while remaining compatible with continuous game solu- tion methods. Here, we investigate the problem of constraint-setting in this context, primarily focusing on a chance-based method. We first motivate these chance constraints in a discrete setting, plac- ing them on 𝑛-player matrix games as a justifiable approach to handling the probabilistic nature of mixing. Then, we describe a numerical solution method for these chance constrained, continu- ous games with simultaneous pure strategy optimization. Finally, using a modified pursuit-evasion game as a motivating example, we demonstrate the actual behavior of this solution method in terms of its fidelity, parameter sensitivity, and efficiency.