Research

Decisions.jl

Decisions.jl is a project to make canonical decision network-backed reprsentations of a wide variety of decision problems, from the most basic Markov decision processes, to rich and expressive multi-agent, semi-Markov, multi-objective extensions, to complex problems unifying decision-, control-, and game-theoretic models.

Conditional Value at Risk for Constrained MDPs

We explore the conjunction of constrained Markov decision processes and conditional-value-at-risk objectives - synthesizing two different modes of safety and risk-averseness - with a mathematical programming based approach.

Locally Optimal Solutions for Integer Programming Games

IPGs, or integer programming games, are n-player games with integer strategy spaces with applications in cybersecurity and transportation. It is difficult to find Nash equilibria in these games, so we described an intuitive and useful near-optimal solution class.

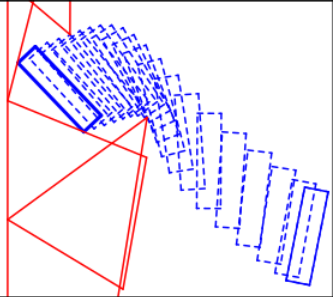
Polyhedral Collision Detection via Vertex Enumeration

In this work we develop a novel bilevel optimization approach to handling polytope collision detection problem, and we show that it may offer reliability and computational benefits in scenarios where contact between two polytope primitives are expected and desired.

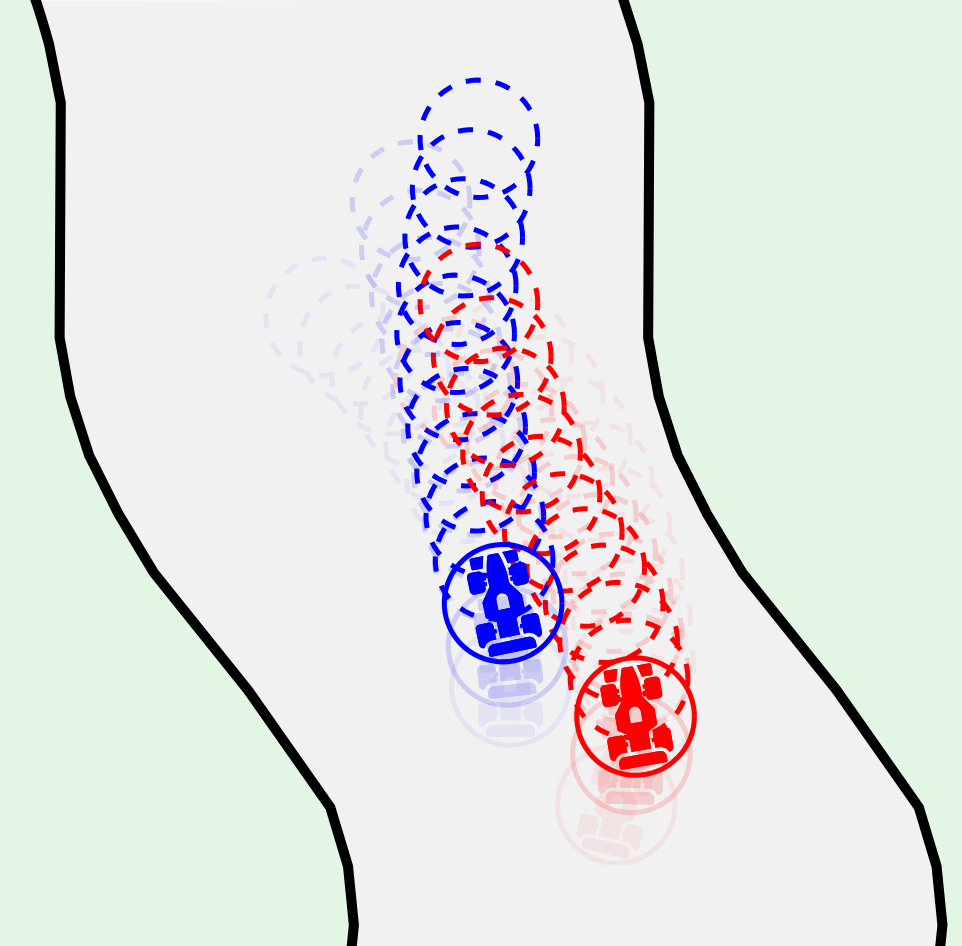
Does bilevel optimization result in more competitive racing behavior?

In this work we explore whether there is competitive benefit to using more complex solution concepts than Nash equilibrium which is most commonly used for its simplicity in the context of competitive racing by means of carrying out a large-scale simulation study where players can choose from different solution concepts without cooperation.

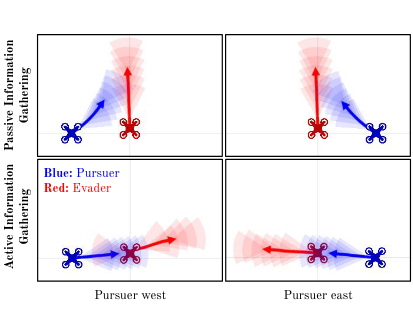
Online Competitive Information Gathering for Partially Observable Trajectory Games

We became interested in partially observable (imperfect information) game theoretic interactions in continuous spaces, like those typically encountered in robotics. This work explores a simple horizon-based approach to seeking good performance in such games.

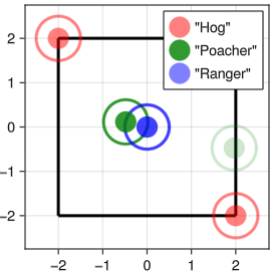
Mixed Strategy Constraints in Continuous Games

Following past research regarding mixed-strategy robot interactions in continuous space, we investigated different ways of setting constraints in these settings without losing the strategic richness given by mixing.